
The Materials Project is an international academic collaboration which is building a database of simulated data on the physical properties of a large number of materials, both existing and predicted ones. The vision is that this aggregated data will enable data-driven approaches to materials discovery, by allowing for computational, rather than (or in tandem with) experimental evaluation of candidate materials for a given application. Given some information on how certain materials perform in a given application, engineers could use the materials database data, together with machine learning algorithms, to find other materials that might perform well, given their calculated properties.
Since the data is freely available (after registering for an API key), I thought it would be interesting to set up a workflow for materials discovery, using as a test case the problem of hemocompatibility of inorganic coating materials.
For many biomedical applications, it is required that the materials used are biocompatible, that is, they do not cause harm to the biological system they come into contact with. Biocompatibility is heavily context-dependent so it is easier to study a more specific problem, in this case hemocompatibility, the degree to which a biomaterial can be brought into contact with the human bloodstram without harming the patient or losing function. In a nutshell, hemocompatibility is directly related to the propensity of a material to cause the formation of blood clots form. The clotting propery of blood is important for the body's healing process, but clotting when it is not necessary can impede bloodflow and lead to loss of organ function and even death. Therefore, a material with high hemocompatibility will be one that leads to a low rate of clot formation when it is introduced to the bloodstream. Since the process of clotting originates with the activation of a type of blood particles called platelets, hemocompatibility studies need to examine the interaction of materials with platelets.
I based myself on an experimental study published by Lackner et al., available here. The authors study the hemocompatibility of a variety of inorganic films deposited on a polymer substrate. There are a variety of experiments that can be related to a material's hemocompatibility; I chose to only include one of them, since this is just a proof of concept.
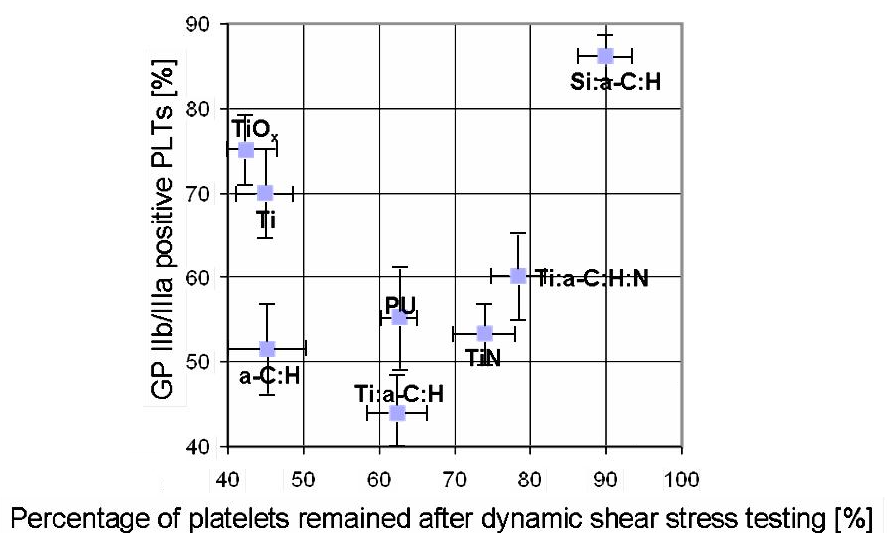
The above figure shows the data from the experimental study. On the horizontal axis is the percentage of platelets that remained bound to the material after a standardized test in which an apparatus was used to try to rub the platelets off the material. A high value means that the adhesion of platelets to the material is strong, which is a positive sign for hemocompatibility, because platelets that attach and then detach from foreign materials are highly likely to induce clotting.
The vertical axis shows the degree of activation of a certain glycoprotein on the platelets that adhered to the material. This activation is a sign of clotting so a low value indicates good hemocompatibility. Therefore, the axis of hemocompatibility goes from the upper left of the graph (bad) to lower right (good).
This data will constitute a (very limited) training set for a machine learning algorithm, which means we need a way of scoring them by their hemocompatibility. I have done this here by simply taking the score to be x-value subtracted by the y-value.
Next we need to decide what data from the Materials Project database to use, for both the materials we have scores for (the training set), and the materials we would like to evaluate using our model. The properties I decided to use were "band_gap", "e_above_hull", (a measure for the stability of the material), "energy_per_atom", and "formation_energy_per_atom". These properties were selected for their convenience (they are all real numbers, which makes them easy to plug into the machine learning algorithm) and because they can all plausibly be related to the stability of the material and its surface, and therefore its hemocompatibility.
(Note: trained physicists might object to the inclusion of the "energy_per_atom" property, on the grounds that it is a physically meaningless number that comes out of a calculation. This is not quite true; while it does not have a direct physical interpretation, it will be correlated with the atomic numbers of the atoms in the unit cell, and therefore will also be correlated to other properties such as the lattice parameter, which might plausibly have an influence on the material's hemocompatibility.)
Things were complicated by the fact that all the materials in the experimental study were deposited from the gas phase, and therefore had amorphous (i.e. not crystalline) structure, which wasn’t the case for any of the materials I could find in the database. I worked around this in the following way: For a given material, gather all the database entries with exactly the same elemental composition, regardless of stoichiometry. Then, for each property I wanted, I simply averaged over all the entries in my filtered set. This is suboptimal of course, as it will include materials that are not very similar to the taget material, but it saved me having to trawl through all the returned entries manually to select only the most appropriate materials.
Once I had the 6 × 4 array containing the averaged properties for each material, I used python’s scikit-learn library to standardize the data (i.e. rescale the properties so that they have similar ranges, which generally improves the numerical stability of the algorithm), and then train a simple linear regression model on it.
We can now use the trained model to predict the hemocompatibility of new materials. I queried the Materials Project database for all materials containing a broad set of elements: {H, C, N, O, Si, P, S, Sc, Ti, V}. Out of the 1426 entries contained in the response of the query, here are the highest scoring ones, after removing volatile gases, pure carbon allotropes, and duplicate entries:
| Chemical Formula | Model Score |
|---|---|
| Si2CN4 | 0.385 |
| Si(CN2)2 | 0.383 |
| Si3N4 | 0.347 |
| Si2N2O | 0.298 |
| P4N6O | 0.262 |
| V6C5 | 0.256 |
| V2C | 0.253 |
| PNO | 0.246 |
| V8C7 | 0.243 |
Note that the top four of these entries contain only elements present in the training set, but in different combinations. This indicates to me that the model, however crude, is at least not obviously inaccurate.
This is obviously a rudimentary analysis, and there are several clear ways to make the results more rigorous. Firstly, implementing cross-validation is a must for any serious machine learning approach to a problem. This means taking some data out of the training set, training the model, and checking that it performs adequately on the removed data (I decided to skip cross-validation since there were only six training samples anyway). In addition, having (much) more training data would vastly improve the predictiveness of the model (see Peter Norvig's article). Finally, the Materials Project data contains much more information per material than the four properties I have used. The other features, such as chemical formula, symmetry group, etc. would add information and therefore possibly improve performance of the machine learning algorithm, but they would need to be transformed to floating point numbers in order to be used.
For those reasons and others, I wouldn't rent lab space to test these results just yet, but it's interesting that such a simple model, trained on so little data, can produce at least a plausible result.
Code for this project can be found here.